Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF Download

Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 7 Integrals chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 7 Integrals Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 7 Integrals exams.

Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers

Plus Two Maths Chapter 7 Integrals question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 7 Integrals chapter wise questions and answers to help them secure good marks in class tests and exams.

Board	Kerala Board
Study Materials	Chapter wise Question and Answers
For Year	2021
Class	12
Subject	Mathematics
Chapters	Maths Chapter 7 Integrals
Format	PDF
Provider	Spandanam Blog

How to check Plus Two Maths Chapter 7 Integrals Question and Answers?

1. Visit our website - https://spandanamblog.com
2. Click on the 'Plus Two Question and Answers'.
3. Look for your 'Plus Two Maths Chapter 7 Integrals Question and Answers'.
4. Now download or read the 'Class 12 Maths Chapter 7 Integrals Question and Answers'.

Plus Two Maths Chapter 7 Integrals Question and Answers PDF Download

We have provided below the question and answers of Plus Two Maths Chapter 7 Integrals Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 7 Integrals Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 7 Integrals, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF. 

Question 1.
Integrate the following. (3 Score each)

1. ∫sin x sin 2x sin 3x dx
2. ∫sec²x cos²2x dx

Answer:
1. We have sin x sin 2x sin 3x
= 1/2 (2 sin x sin 3x) sin 2x
= 1/2 (cos 2x – cos 4x) sin 2x
= 1/4 (2 sin 2x cos 2x – 2 cos 4x sin 2x)
= 1/4 [sin 4x – (sin 6x – sin 2x)]
= 1/4(sin 4x + sin 2x – sin 6x)
∫sin x sin 2x sin 3x dx
= \(\frac{1}{4}\) ∫(sin 4x + sin 2x – sin 6x) dx
= –\(\frac{1}{16}\) cos 4x – \(\frac{1}{8}\) cos 2x + \(\frac{1}{24}\) cos 6x + c.

2. sec²x cos²2x = \(\frac{\left(2 \cos ^{2} x-1\right)^{2}}{\cos ^{2} x}\)
= \(\left(\frac{2 \cos ^{2} x}{\cos x}-\frac{1}{\cos x}\right)^{2}\) = (2cosx – secx)²
= 4cos²x + sec²x – 4
= 2(1 + cos2x) + sec²x – 4
= 2cos2x + sec²x – 2
∫sec² x cos² 2x dx = ∫(2 cos 2x + sec² x – 2)dx
= sin 2x + tan x – 2x + c.

Question 2.
Find \(\int \frac{2+\sin 2 x}{1+\cos 2 x} e^{x} d x\)?
Answer: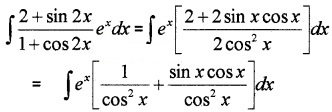

= ∫e^x [sec² x + tan x]dx
= ∫e^x[tanx + sec²x]dx = e^x tanx + c.

Question 3.
Evaluate \(\int \frac{\sec ^{2} x d x}{\sqrt{\tan ^{2} x+4}}\)?
Answer:
Put tanx = u, sec²xdx = dy

Question 4.
Find the following integrals.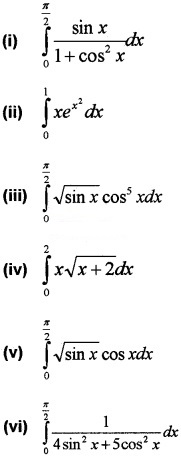

Answer:
(i) I = \(\int_{0}^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^{2} x} d x\)
Put cosx = t ⇒ -sin xdx = dt
When x = 0 ⇒ t = cos0 = 1,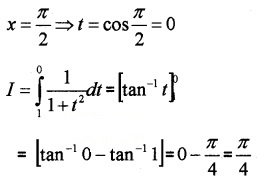

(ii) I = \(\int_{0}^{1} x e^{x^{2}} d x\)
Put x² = t ⇒ 2xdx = dt
When x = 0 ⇒ t = 0,
x = 1 ⇒ t = 1
I = \(\frac{1}{2} \int_{0}^{1} e^{t} d t\) =

= [e¹ – e⁰] = e – 1.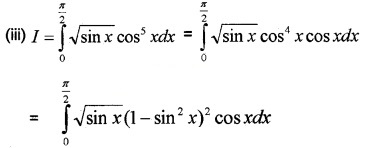

Put sin x = t ⇒ cos xdx = dt
When x = 0 ⇒ t = sin0 = 0,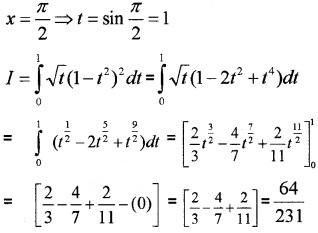

(iv) I = \(\int_{0}^{2} x \sqrt{x+2} d x\)
Put x + 2 = t² ⇒ dx = 2tdt
When x = 0 ⇒ t = \(\sqrt{2}\), x = 2 ⇒ t = 2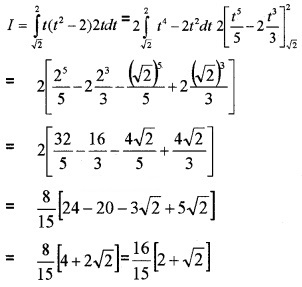

(v) I = \(\int_{0}^{\frac{\pi}{2}} \sqrt{\sin x} \cos x d x\)
Put sin x = t ⇒ cos xdx = dt
When x = 0 ⇒ t = sin0 = 0,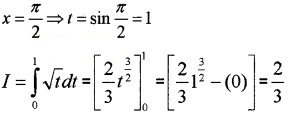


Put tan x = t ⇒ sec² xdx = dt
When x = 0 ⇒ t = tan 0 = 0,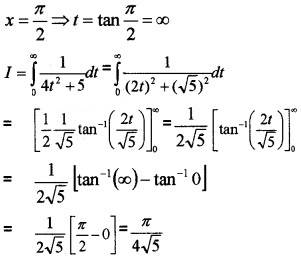

Question 5.
(i) If f (x) is an odd function, then \(\int_{-a}^{a} f(x)\) = ?
(a) 0
(b) 1
(c) 2\(\int_{0}^{a} f(x)\) dx
(d) 2a
Evaluate
(ii) \(\int_{-\pi / 2}^{\pi / 2} \sin ^{99} x \cdot \cos ^{100} x d x\)
(iii) \(\int_{-1}^{1} e^{|x|} d x\)
Answer:
(i) (a) 0.

(ii) Here, f(x) = sin⁹⁹x.cos¹⁰⁰x .then,
f(-x) = sin⁹⁹(- x).cos¹⁰⁰(- x) = – sin⁹⁹ x. cos¹⁰⁰ x = -f(x)
∴ odd function ⇒ \(\int_{-\pi / 2}^{\pi / 2} \sin ^{99} x \cdot \cos ^{100} x d x=0\).

(iii) Here, f(x) = e^|x|, f(-x) = e^|-x| = e^|x| = f(x)
∴ even function.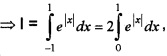

we have |x| = x, 0 ≤ x ≤ 1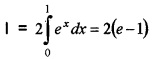

Question 6.

1. Show that cos² x is an even function. (1)
2. Evaluate \(\int_{-\pi / 4}^{\pi / 4} \cos ^{2} x d x\) (2)

Answer:
1. Let f(x) = cos²x ⇒ f(-x) = cos² (-x) = cos² x = f(x) even.

2.

Question 7.
Find the following integrals.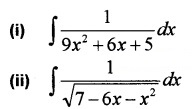

Answer: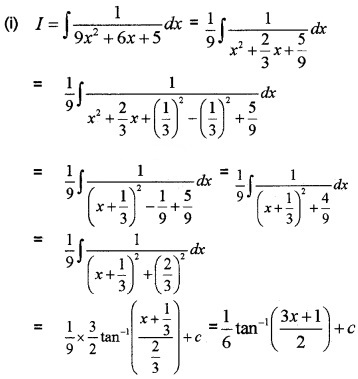

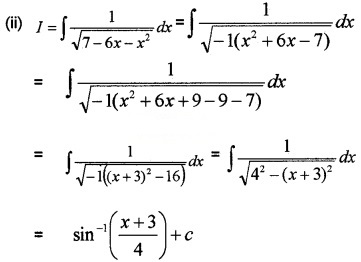
Question 8.
Find the following integrals.

Answer: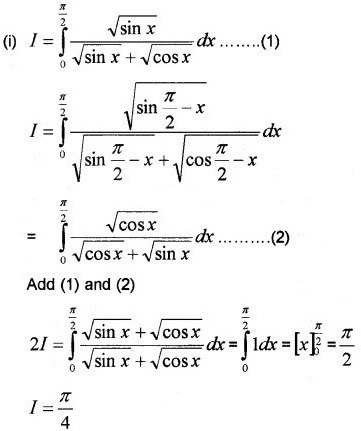


Add (1) and (2)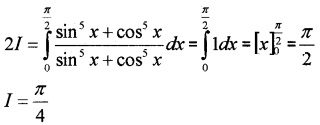

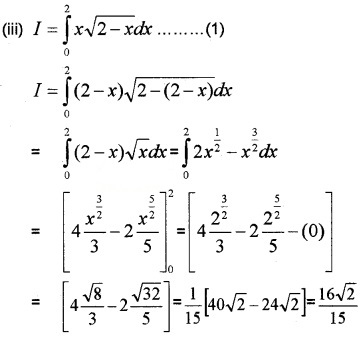
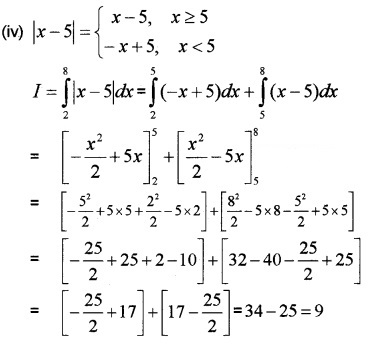
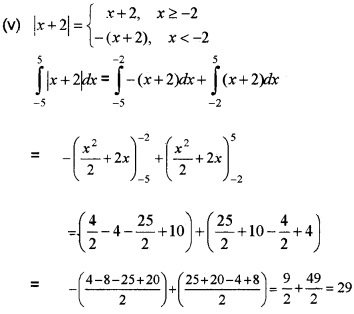
Question 9.
Find the following integrals.

1. \(\int \frac{1}{3+\cos x} d x\)
2. \(\int \frac{2 x}{x^{2}+3 x+2} d x\)

Answer:
1. \(\int \frac{1}{3+\cos x} d x\)
Put t = tanx/2 ⇒ dt = 1/2 sec² x/2 dx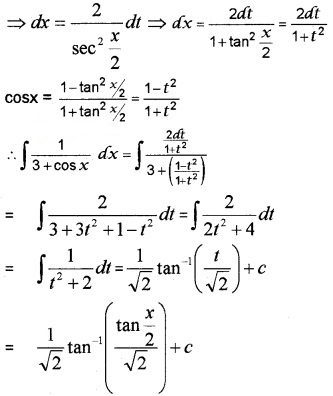

2. \(\int \frac{2 x}{x^{2}+3 x+2} d x\) = \(\int \frac{2 x}{(x+2)(x+1)} d x\)

2x = A(x + 1) + B (x + 2)
when x = -1, -2 = B ; B = -2
when x = -2, -4 = -A ; A = 4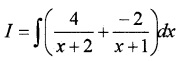

= 4log(x + 2) – 2log (x + 1) + C.

Plus Two Maths Integrals Four Mark Questions and Answers

Question 1.
Find the following integrals.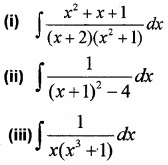

Answer:

x² + x +1 = A(x² + 1) + (Bx + C)(x + 2)
Put x = -2 ⇒ 4 – 2 + 1 = 5A ⇒ A = \(\frac{3}{5}\)
Equating the coefficients of x²
⇒ 1 = A + B ⇒ B = 1 – \(\frac{3}{5}\) = \(\frac{2}{5}\)
Equating the constants
⇒ 1 = A + 2C ⇒ 2C = 1 – \(\frac{3}{5}\) = \(\frac{2}{5}\) ⇒ C = \(\frac{1}{5}\)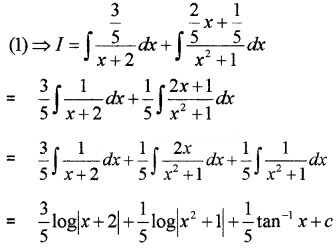

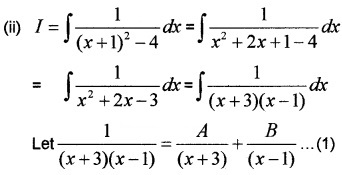
⇒ 1 = A(x – 1) + B(x + 3)
Put x = 1 ⇒ 1 = 2A ⇒ A = \(\frac{1}{2}\)
Put x = -3 ⇒ 1 = -4B ⇒ B = – \(\frac{1}{4}\)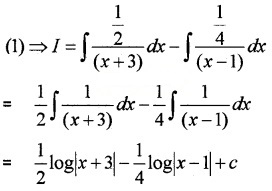

Equating the constants; ⇒ 1 = A
Equating the coefficients if t;
⇒ 0 = A + B ⇒ B = -1

Question 2.
Find the following integrals.

1. ∫ e^2x sin3xdx
2. ∫ x sin^-1xdx

Answer:
1. I = ∫e^2x sin3xdx = ∫ sin 3x × e^2xdx

2. ∫ x sin^-1xdx = ∫ sin^-1x × xdx

Question 3.
(i) Which of the following is the value of \(\int \frac{d x}{\sqrt{a^{2}-x^{2}}}\)? (1)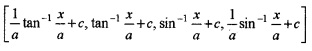

(ii) Evaluate \(\int \frac{2 x}{x^{2}+3 x+2} d x\) (3)
Answer:
(i) [sin^-1\(\frac{x}{a}\) + c]

(ii)

⇒ 2x = A(x + 1) + B(x + 2) ⇒
Put x = -2 and x = -1, we get A = 4, B = -2

Question 4.

1. Choose the correct answer from the bracket.
   ∫e^x dx = — (e^2x + c, e^-x + c, e^2x + c) (1)
2. Evaluate: ∫ e^x sin x dx

Answer:
1. e^x + c

2. I = ∫e^x sinxdx = sinx.e^x – ∫cos x.e^xdx
= sin x.e^x – (cos x.e^x – ∫(- sin x).e^x dx)
= sinx.e^x – cosxe^x – ∫sinx.e^xdx
= sin x.e^x – cos xe^x – I
2I = sin x.e^x – cos xe^x
I = \(\frac{1}{2}\)e^x(sinx – cosx) + c.

Question 5.
(i) f(x)∫g(x) dx – ∫(f'(x)∫g(x) dx)dx (1)
(a) ∫f'(x)g{x)dx
(b) ∫f(x)g'(x)dx
(c) ∫\(\frac{f(x)}{g(x)}\)dx
(d) ∫f(x)g(x)dx
(ii) Integrate sin^-1\(\sqrt{\frac{x}{a+x}}\)dx w.r.to x. (3)
Answer:
(i) (d) ∫f(x)g(x)dx

(ii) ∫sin^-1\(\sqrt{\frac{x}{a+x}}\)dx,
Put x = a tan²θ, θ = tan^-1\(\sqrt{\frac{x}{a}}\)
⇒ dx = 2a tanθ sec²θ dθ
I = ∫sin^-1\(\left(\frac{\tan \theta}{\sec \theta}\right)\) 2a tanθ sec²θ dθ
= ∫sin^-1(sinθ)2a tanθ sec²θ dθ
= 2a∫θ tanθ sec²θ dθ
Put tanθ = t, θ = tan^-1 t ⇒ sec²θ dθ = dt
= 2a ∫ tan^-1 t (t) dθ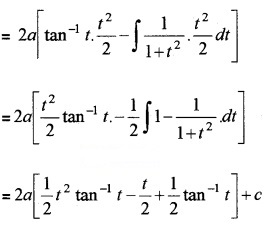

= a[tan²θ.θ – tanθ + θ] + c
= a[θ(1 + tan²θ) – tanθ] + c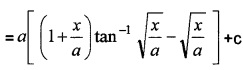

Question 6.
Match the following. (4)

Answer:

Question 7.
Evaluate \(\int \frac{x}{\sqrt{x+a}+\sqrt{x+b}} d x\)?
Answer:

Question 8.
Match the following.

Answer:
1.

2. ∫sec x(sec x + tan x)dx = ∫(sec² x + sec x. tan x)dx
= tanx + secx + c.

3. ∫e^3xdx = \(\frac{e^{3 x}}{3}\) + c.

4. ∫(sin x + cos x)dx = sin x – cosx + c.

Question 9.
Consider the integral I = \(\int \frac{x \sin ^{-1} x}{\sqrt{1-x^{2}}} d x\)?

1. What substitution can be given for simplifying the above integral? (1)
2. Express I in terms of the above substitution. (1)
3. Evaluate I. (2)

Answer:
1. Substitute sin^-1 x = t.

2. We have, sin^-1 x = t ⇒ x = sint
Differentiating w.r.t. x; we get,
\(\frac{1}{\sqrt{1-x^{2}}}\)dx = dt
∴ I = ∫t sin t dt.

3. I = ∫t sin t dt = t.(-cost) -∫(-cost)dt = -t cost + sint + c
= -sin^-1 x. cos (sin^-1 x) + sin(sin^-1 x) + c
x – sin^-1 x.cos(sin^-1 x) + c.

Question 10.
Evaluate \(\int_{0}^{\pi / 4} \log (\tan x) d x\).
Answer:

Question 11.
Find the following integrals.

1. \(\int \frac{\sec ^{2} x}{\cos e c^{2} x} d x\) (2)
2. \(\int \frac{1}{x^{2}-6 x+13} d x\) (2)

Answer:
1. \(\int \frac{\sec ^{2} x}{\cos e c^{2} x} d x\) = \(\int \frac{\sin ^{2} x}{\cos ^{2} x} d x\) = ∫tan² xdx
= ∫(sec²x – 1)dx = tanx – x + c.

2. \(\int \frac{1}{x^{2}-6 x+13} d x\)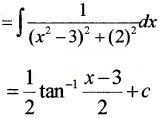

Question 12.
Match the following. Justify your answer.

Answer:

Question 13.
(i) ∫sin2x dx = ? (1)
(a) 2 cos x + c
(b) -2 sin x + c
(c) \(\frac{\cos 2 x}{2}\) + c
(d) \(-\frac{\cos 2 x}{2}\) + c
(ii) Evaluate ∫e^x sin 2x dx (3)
Answer:
(i) (d) \(-\frac{\cos 2 x}{2}\) + c.

(ii) Consider I = ∫e^x sin 2x dx
= ∫sin 2x. e^xdx = sinx.e^x – 2∫cos 2x. e^xdx
= sin 2x.e^x – 2 (cos 2x.e^x + 2∫sin 2x. e^xdx)
= sin 2x. e^x – 2 cos 2x e^x – 4 ∫sin 2x. e^xdx
= sin 2x. e^x – 2 cos 2x e^x – 4I
5 I = sin 2x. e^x – 2 cos 2x e^x
I = \(\frac{e^{x}}{5}\) (sin 2x – 2 cos 2x).

Question 14.

1. Resolve \(\frac{x^{2}+1}{x^{2}-5 x+6}\) into partial fractions. (2)
2. Hence evaluate ∫\(\frac{x^{2}+1}{x^{2}-5 x+6}\). (2)

Answer:
1.

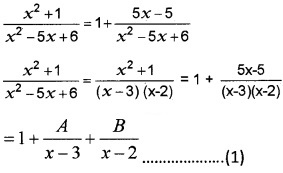
2.

5x – 5 = A(x – 2) + B(x – 3)
x = 2, 5 = -B, B = -5
x = 3, 10 = A, A = 10
(1) ⇒ I = ∫ 1dx + ∫\(\frac{10}{x-3}\) dx – ∫\(\frac{5}{x-2}\) dx
= x + 10log(x – 3) – 5log(x – 2) + c.

Question 15.
Evaluate \(\int_{0}^{4}\) xdx as a limit of sum.
Answer:
By definition,
\(\int_{a}^{b}\) f(x) dx =
(b – a)\(\lim _{n \rightarrow \infty} \frac{1}{n}\){f(a) + f(a + h) +…….+f(a + {n – 1)h)}
Here, a = 0, b = 4, f(x) = x, h = \(\frac{4-0}{n}=\frac{4}{n}\) ⇒ nh = 4

Question 16.

1. Define the real valued function f(x) = |x² + 2x – 3| (2)
2. Evaluate \(\int_{0}^{2}\)|x² + 2x – 3|dx. (2)

Answer:
1. f(x) = |x² + 2x – 3| = |(x – 1) (x + 3)|
We have;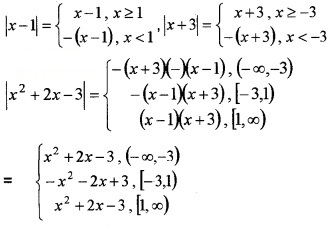

2. I = \(\int_{0}^{2}\)|x² + 2x – 3|dx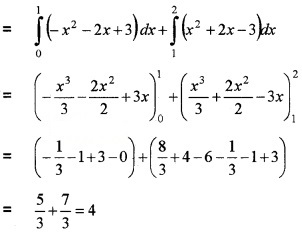

Question 17.
Consider the function f(x) = |x|+|x + 1|

1. Define the function f (x) in the interval [-2, 1]. (2)
2. Find the integral \(\int_{-2}^{1}\) f(x) dx (2)

Answer:
1. Given, f(x) = |x|+|x + 1|.
We have,

Combining these two functions, we get the function f(x).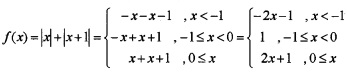

2.

Question 18.
Evaluate \(\int_{\sqrt{6}}^{\sqrt{3}} \frac{d x}{1+\sqrt{\tan x}} d x\). (4)
Answer:

Plus Two Maths Integrals Six Mark Questions and Answers

Question 1.
(i) Fill in the blanks. (3)
(a) ∫ tan xdx = —
(b) ∫ cos xdx = —
(c) ∫\(\frac{1}{x}\)dx = —
(ii) Evaluate ∫sin³ xcos² xdx (3)
Answer:
(i) (a) log|secx| + c
(b) sinx + c
(c) log|x| + c.

(ii) ∫sin³ xcos² xdx = ∫sin² xcos² x sin xdx
= ∫(1 – cos² x)cos² x sin xdx
Put cos x = t ⇒ – sin xdx = dt
∴ ∫(1 – cos² x)cos² xsin xdx = -∫(1 – t² )t²dt
= ∫(t⁴ – t²)dt = \(\frac{t^{5}}{5}-\frac{t^{3}}{3}\) + c
= \(\frac{\cos ^{5} x}{5}-\frac{\cos ^{3} x}{3}\) + c.

Question 2.
Find the following integrals.

Answer:
(i) I = ∫(3x – 2)\(\sqrt{x^{2}+x+1} d x\)
Let 3x – 2 = A(2x + 1) + B
⇒ 3 = 2 A ⇒ A = \(\frac{3}{2}\)
⇒ -2 = A + B ⇒ -2 = \(\frac{3}{2}\) + B
⇒ B = -2 – \(\frac{3}{2}\) = – \(\frac{7}{2}\)

Using (2) and (3) in (1) we have;

(ii) I = \(\int \frac{2 x-3}{x^{2}+3 x-18} d x\)
Let 2x – 3 = A(2x + 3) + B
⇒ 2 = 2A ⇒ A = 1
⇒ -3 = 3A + B ⇒ -3 = 3 + B ⇒ B = -6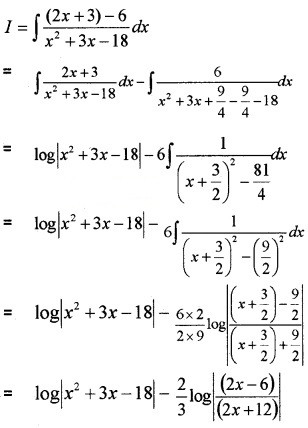

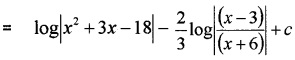
(iii) I = \(\int \frac{5 x+2}{1+2 x+3 x^{2}} d x\)
Let 5x + 2 = A{6x + 2) + B
⇒ 5 = 6 A ⇒ A = \(\frac{5}{6}\)
⇒ 2 = 2A + B ⇒ 2 = \(\frac{5}{3}\) + B ⇒ 2 – \(\frac{5}{3}\) = \(\frac{1}{3}\)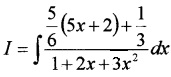

(iv) I = \(\int \frac{5 x+3}{\sqrt{x^{2}+4 x+10}} d x\)
Let 5x + 3 = A(2x + 4) + B
⇒ 5 = 2A ⇒ A = \(\frac{5}{2}\)
⇒ 3 = 4A + B ⇒ 3 = 10 + B ⇒ B = -7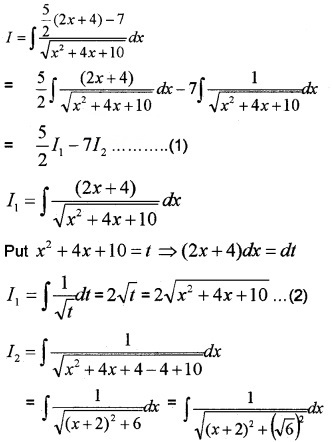

Using (2) and (3) in (1) we have;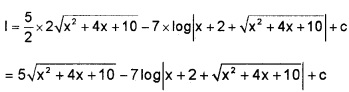

Question 3.
Consider the expression \(\frac{1}{x^{3}-1}\)

1. Split it into partial fraction. (2)
2. Evaluate ∫ \(\frac{1}{x^{3}-1}\) dx (4)

Answer:
1.

1 = A (x² + x + 1) + (Bx + c)(x + 1),
Put x = -1 ⇒ 1 = A(1 + 1 + 1) ⇒ A= \(\frac{1}{3}\)
Equating like terms.
0 = A + B ⇒ B = – \(\frac{1}{3}\), 1 = A + C ⇒ C = \(\frac{2}{3}\)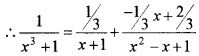

2.

Put, x – 2 = D (2x – 1) + E ,
1 = 2 D ⇒ D = \(\frac{1}{2}\),
-2 = -D + E ⇒ E = –\(\frac{3}{2}\)

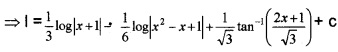
Question 4.
(i) Match the following (4)

(ii) Consider the function f(x) = \(\frac{x^{4}}{x+1}\) Evaluate ∫f(x)dx (2)
Answer:
(i)

(ii) Here the numerator is of degree 4 and denominator of degree 1. So to make it a proper fraction we have to divide Nr by Dr.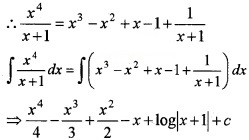

Question 5.

1. Evaluate the as \(\int_{0}^{2}\)x²dx the limit of a sum. (3)
2. Hence evaluate \(\int_{-2}^{2}\)x²dx (1)
3. If \(\int_{0}^{2}\) f(x)dx = 5 and \(\int_{-2}^{2}\) f(x)dx = 0, then \(\int_{-2}^{0}\) f(x)dx = …….. (2)

Answer:
1. Here the function is f(x) = x², a = 0, b = 2 and h = \(\frac{b-a}{n}=\frac{2}{n}\)
\(\int_{0}^{2}\)x²dx =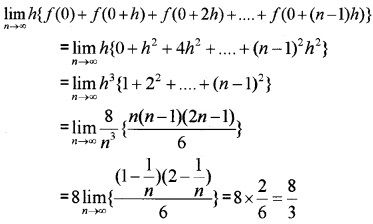

2. \(\int_{-2}^{2}\) x²dx = 2 \(\int_{0}^{2}\)x²dx = \(\frac{16}{3}\)

3.

Question 6.
Find ∫\(\sqrt{\tan x}\)xdx.
Answer:
Given;
I = ∫\(\sqrt{\tan x}\)xdx,
Put tanx = t² ⇒ sec²xdx = 2tdt ⇒ dx = \(\frac{2 t d t}{1+t^{4}}\)

Question 7.
(i) Match the following. (2)

(ii) Integrate \(\frac{\sec ^{2} x}{5 \tan ^{2} x-12 \tan x+14}\) w.r.to x. (4)
Answer:
(i)

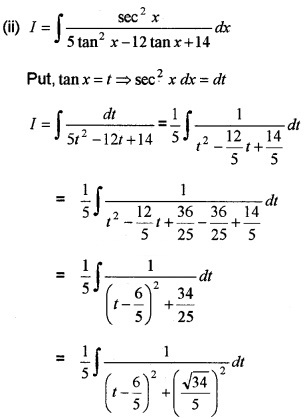
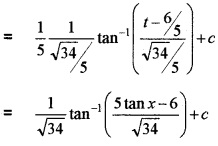
Question 8.

1. Evaluate \(\int_{0}^{1} \sqrt{x} d x\) (1)
2. If \(\int_{0}^{a} \sqrt{x} d x=2 a \int_{0}^{\pi / 2} \sin ^{3} x d x\), find the value of a. (3)
3. Hence find \(\int_{a}^{a+1}\)x dx. (2)

Answer:
1.

2. Given;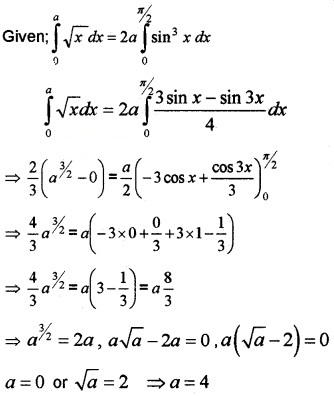

3. When a = 0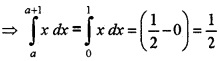

When a = 4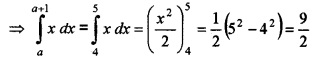

Question 9.
(i) Let f (x) be a function, then \(\int_{0}^{a}\) f(x) dx = ? (1)
(a) 2 \(\int_{0}^{a}\) f(x – a) dx
(b) \(\int_{0}^{a}\) f(a – x) dx
(c) f(a)
(d) 2\(\int_{0}^{a}\) f(a – x) dx
Evaluate

Answer:
(i) (b) \(\int_{0}^{a}\) f(a – x) dx

(ii)

(1) + (2)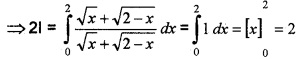

⇒ I = 1.

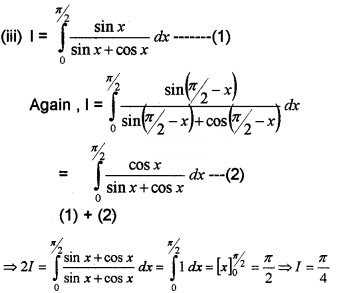
Question 10.
Find the following integrals.

1. ∫\(\frac{2 e^{x}}{e^{3 x}-6 e^{2 x}+11 e^{x}-6} d x\)
2. ∫\(\frac{(3 \sin x-2) \cos x}{5-\cos ^{2} x-4 \sin x} d x\)

Answer:
1.

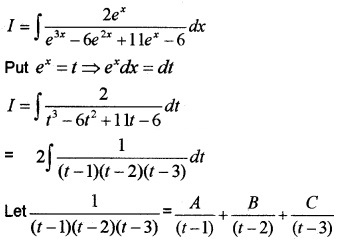
⇒ 1 = A(t – 2)(t – 3) + B(t – 1)(t – 3) + C(t – 1)(t – 2)
Put t = 1 ⇒ 1 = A(-1)(-2) ⇒ A = \(\frac{1}{2}\)
Put t = 2 ⇒ 1 = B(1)(-1) ⇒ B = -1
Put t = 3 ⇒ 1 = B(2)(1) ⇒ B = \(\frac{1}{2}\)

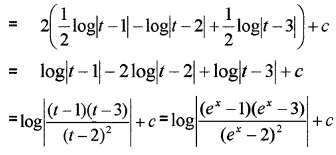
2. I = ∫\(\frac{(3 \sin x-2) \cos x}{5-\cos ^{2} x-4 \sin x} d x\)dx
Put sin x = t ⇒ cosxdx = dt

⇒ 3t – 2 = A(t – 2) + B
Equating the coefficients if t; ⇒ 3 = A
Equating the constants
⇒ -2 = -2A + B ⇒ -2 = -6 + B ⇒ B = 4

Question 11.

1. Find ∫\(\frac{1}{x^{2}+a^{2}}\)dx (1)
2. Show that 3x + 1 = \(\frac{3}{4}\)(4x – 2) + \(\frac{5}{2}\) (2)
3. Evaluate \(\int \frac{3 x+1}{2 x^{2}-2 x+3} d x\) (3)

Answer:
1. ∫\(\frac{1}{x^{2}+a^{2}}\)dx = 1/a tan^-1 x/a + c.

2. 3x + 1 = A \(\frac{d}{d x}\)(2x² – 2x + 3) + B
= A(4x – 2) + B
3 = 4A; A = 3/4
1 = -2A + B
1 = -3/2 + B, B = 1 + 3/2 = 5/2
∴ 3x + 1 = 3/4(4x – 2) + 5/2

3.

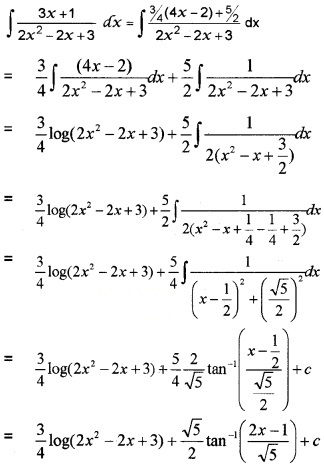
Plus Two Mathematics All Chapters Question and Answers

• Plus Two Mathematics Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF

Benefits of the Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF

The Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF.

FAQ’s Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF

Where can I download Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF?

You can download Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF for the latest 2021 session.

Can I download Plus Two All subjects Question and Answers PDF?

Yes - You can click on the links above and download subject wise question papers in PDF

Is there any charge for the Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF?

There is no charge for the model papers for you can download everything free