Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF Download

Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF Download: Students of Standard 12 can now download Plus Two Maths Chapter 4 Determinants chapter wise question and answers pdf from the links provided below in this article. Plus Two Maths Chapter 4 Determinants Question and Answer pdf will help the students prepare thoroughly for the upcoming Plus Two Maths Chapter 4 Determinants exams.

Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers

Plus Two Maths Chapter 4 Determinants question and answers consists of questions asked in the previous exams along with the solutions for each question. To help them get a grasp of chapters, frequent practice is vital. Practising these questions and answers regularly will help the reading and writing skills of students. Moreover, they will get an idea on how to answer the questions during examinations. So, let them solve Plus Two Maths Chapter 4 Determinants chapter wise questions and answers to help them secure good marks in class tests and exams.

Board	Kerala Board
Study Materials	Chapter wise Question and Answers
For Year	2021
Class	12
Subject	Mathematics
Chapters	Maths Chapter 4 Determinants
Format	PDF
Provider	Spandanam Blog

How to check Plus Two Maths Chapter 4 Determinants Question and Answers?

1. Visit our website - https://spandanamblog.com
2. Click on the 'Plus Two Question and Answers'.
3. Look for your 'Plus Two Maths Chapter 4 Determinants Question and Answers'.
4. Now download or read the 'Class 12 Maths Chapter 4 Determinants Question and Answers'.

Plus Two Maths Chapter 4 Determinants Question and Answers PDF Download

We have provided below the question and answers of Plus Two Maths Chapter 4 Determinants Chapter wise study material which can be downloaded by you for free. These Plus Two Maths Chapter 4 Determinants Chapter Wise Question and answers will contain important questions and answers and have been designed based on the latest Plus Two Maths Chapter 4 Determinants, books and syllabus. You can click on the links below to download the Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF. 

Question 1.
Using properties of determinants prove \(\left|\begin{array}{ccc}{x} & {y} & {x+y} \\{y} & {x+y} & {x} \\{x+y} & {x} & {y}\end{array}\right|\) = -2(x³ + y³).
Answer: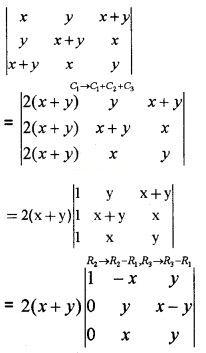

= 2(x + y)(-x² + xy – y²) = -2(x³ + y³).

Question 2.
If a, b, c are real numbers and \(\left|\begin{array}{lll}{b+c} & {c+a} & {a+b} \\{c+a} & {a+b} & {b+c} \\{a+b} & {b+c} & {c+a}\end{array}\right|\) = 0, Show that a = b = c.
Answer:

2(a + b + c) [(b – c) (c – b) – (b – a) (c – a)] =0 (a+b+c) = 0
(a + b + c) = 0 or (b – c) (c – b) = (b – a) (c – a)
(a + b + c) = 0 or a = b = c.

Question 3.
Solve using properties of determinants.
\(\left|\begin{array}{ccc}{2 x-1} & {x+7} & {x+4} \\{x} & {6} & {2} \\{x-1} & {x+1} & {3}
\end{array}\right|\) = 0
Answer:

⇒ (x – 1) (x² + x – 6x + 6) = 0
⇒ (x – 1)(x² – 5x + 6) = 0
⇒ (x – 1) (x – 3) (x – 2) = 0
⇒ x = 1, x = 3, x = 2.

Question 4.
If \(\left|\begin{array}{cc}{3} & {x} \\{x} & {x}\end{array}\right|=\left|\begin{array}{cc}{-2} & {2} \\{4} & {1}\end{array}\right|\), find the value of x.
Answer:
\(\left|\begin{array}{cc}{3} & {x} \\{x} & {x}\end{array}\right|=\left|\begin{array}{cc}{-2} & {2} \\{4} & {1}\end{array}\right|\)
⇒ 3x – x² = – 2 – 8
⇒ x² – 3x – 10 = 0
⇒ x = 5, -2.

Question 5.
A = \(\left[\begin{array}{ccc}{1} & {-3} & {1} \\{2} & {0} & {4} \\{1} & {2} & {-2}
\end{array}\right]\)

1. Calculate |A| (1)
2. Find |adjA| {Hint: using the property A × adjA = |A|I} (1)
3. Find |3A| (1)

Answer:
1. |A| = \(\left[\begin{array}{ccc}{1} & {-3} & {1} \\{2} & {0} & {4} \\{1} & {2} & {-2}
\end{array}\right]\) = – 28.

2. A × adjA = |A|I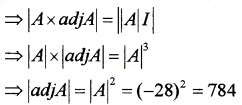

3. |3A| = 27 × |A| = 27 × -28 = -756.

Question 6.
Using properties of determinants proves the following.

Answer:

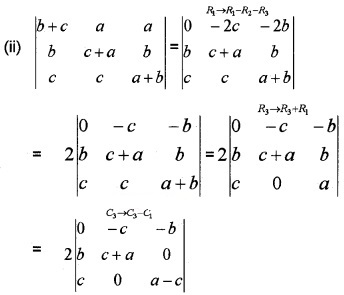
= 2{-{-c){b{a – c)) – b(-c(c + a))}
= 2{c(ab – cb) + b(c² + ac)}
= 2{abc – c²b + bc² + abc)} = 4abc.

Plus Two Maths Determinants Four Mark Questions and Answers

Question 1.
(i) If \(\left|\begin{array}{rrr}{1} & {-3} & {2} \\{4} & {-1} & {2} \\{3} & {5} & {2}\end{array}\right|\) = 40, then \(\left|\begin{array}{ccc}{1} & {4} & {3} \\{-3} & {-1} & {5} \\{2} & {2} & {2}\end{array}\right|\) = ?
(a) 0
(b) – 40
(c) 40
(d) 2 (1)
(ii) \(\left|\begin{array}{rrr}{3} & {-3} & {2} \\{12} & {-1} & {2} \\{9} & {5} & {2}\end{array}\right|\) = ?
(a) 120
(b) 40
(c) – 40
(d) 0 (1)
(iii) Show that ∆ = \(\left|\begin{array}{ccc}{-a^{2}} & {a b} & {a c} \\{b a} & {-b^{2}} & {b c} \\{a c} & {b c} & {-c^{2}}\end{array}\right|\) = 4a²b²c² (2)
Answer:
(i) (c) 40

(ii) (a)120

(iii) ∆ = abc\(\left|\begin{array}{ccc}{-a} & {a} & {a} \\{b} & {-b} & {b} \\{c} & {c} & {-c}\end{array}\right|\) take a, b, c from C₁, C₂, C₃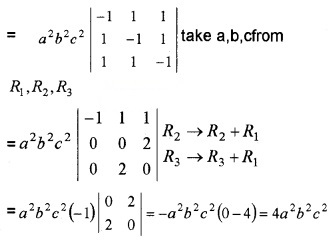

Question 2.

Answer:
(i) \(\left|\begin{array}{ll}{2} & {4} \\{5} & {1}\end{array}\right|=\left|\begin{array}{ll}{2 x} & {4} \\{6} & {x}\end{array}\right|\) ⇒ -18 = 2x² – 24.
⇒ 2x² = 6 ⇒ x² = 3 ⇒ x = \(\pm \sqrt{3}\).

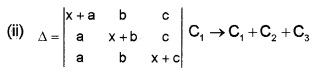
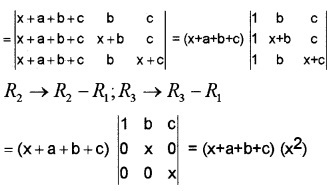
Question 3.
Prove that \(\left|\begin{array}{ccc}{(b+c)^{2}} & {a^{2}} & {a^{2}} \\{b^{2}} & {(c+a)^{2}} & {b^{2}} \\{c^{2}} & {c^{2}} & {(a+b)^{2}}\end{array}\right|\) = 2abc(a + b + c)³.
Answer:

= (a + b + c)² × 2ab [(b + c) (c + a) – ab]
= (a + b + c)² × 2ab [bc + ab + c² + ac – ab)
= (a + b + c)² × 2abc [a + b + c]
= 2abc (a + b + c)³.

Question 4.
(i) Let the value of a determinant is ∆. Then the value of a determinant obtained by interchanging two rows is
(a) ∆
(b) -∆
(c) 0
(d) 1 (1)
(ii) Show that \(\left|\begin{array}{ccc}{a+b} & {b+c} & {c+a} \\{b+c} & {c+a} & {a+b} \\{c+a} & {a+b} & {b+c}\end{array}\right|=2\left|\begin{array}{lll}{a} & {b} & {c} \\{b} & {c} & {a} \\{c} & {a} & {b}\end{array}\right|\) (3)
Answer:
(i) (b) -∆

(ii) Operating C₁ → C₁ + C₂ + C₃, we have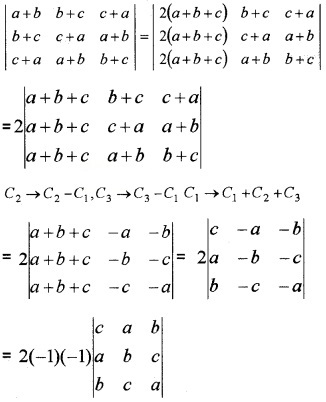

Question 5.
Test the consistency 3x – y – 2z = 2, 2y – z = -1, 3x – 5y = 3.
Answer:
The given system of equations can be put in the matrix form, AX = B, where

|A| = 3(0 – 5) + 1(0 + 3) – 2(0 – 6) = 0
C₁₁ = -5, C₁₂ = -3, C₂₁ = -6, C₂₂ = 10, C₂₃ = 6, C₃₁ = 12, C₃₂ = 5, C₃₃ = 6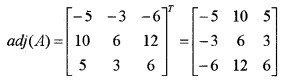

Therefore the system is inconsistent and has no solutions.

Question 6.
Consider the system of equations 2x – 3y = 7 and 3x + 4y = 5

1. Express the system in AX = B form. (1)
2. Find adj A (2)
3. Solve the system of equations. (1)

Answer:
1. |A| = \(\left|\begin{array}{cc}{2} & {-3} \\{3} & {4}\end{array}\right|\) = 8 + 9 = 17.

2. c₁₁ = 4, c₁₂ = -3, c₂₁ = 3, c₂₂ = 2,

3. The given equations can be expressed in the form AX = B,

Question 7.
(i) If A and B are matrices of order 3 such that|A| = -1; |B| = 3, then |3AB| is
(a) -9
(b) -27
(c) -81
(d) 9 (1)
(ii) If A = \(\left[\begin{array}{cc}{1} & {\tan x} \\{-\tan x} & {1}\end{array}\right]\), Show that A^T A^-1 = \(\left[\begin{array}{cc}{\cos 2 x} & {-\sin 2 x} \\{\sin 2 x} & {\cos 2 x}\end{array}\right]\) (3)
Answer:
(i) (c) -81 (since |3AB| = 27|A||B|).

(ii) |A| = \(\left[\begin{array}{cc}{1} & {\tan x} \\{-\tan x} & {1}\end{array}\right]\) = sec²x ≠ 0, therefore A is invertible.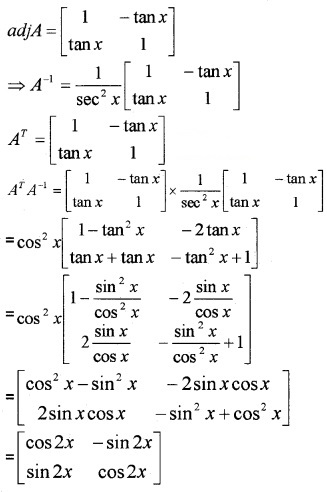

Question 8.
Consider the determinant ∆ = \(\left|\begin{array}{ccc}{x} & {x^{2}} & {1+x^{3}} \\{y} & {y^{2}} & {1+y^{3}} \\{z} & {z^{2}} & {1+z^{3}}\end{array}\right|\), Where x, y, z, are different.
(i) Express the above determinant as sum of two determinants. (1)
(ii) Show that if ∆ = 0, then 1 + xyz = 0. (3)
Answer:
(i) Given,
∆ = \(\left|\begin{array}{ccc}{x} & {x^{2}} & {1+x^{3}} \\{y} & {y^{2}} & {1+y^{3}} \\{z} & {z^{2}} & {1+z^{3}}\end{array}\right|=\left|\begin{array}{ccc}{x} & {x^{2}} & {1} \\{y} & {y^{2}} & {1} \\{z} & {z^{2}} & {1}\end{array}\right|+\left|\begin{array}{ccc}{x} & {x^{2}} & {x^{3}} \\{y} & {y^{2}} & {y^{3}} \\{z} & {z^{2}} & {z^{3}}\end{array}\right|\)

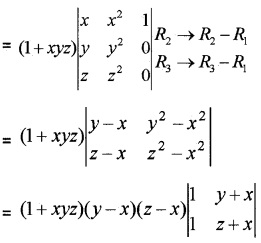
Given, ∆ = 0 ⇒ (1 + xyz)(y – x)(z – x)(z – y) = 0 ⇒ 1 + xyz = 0
∵ x ≠ y ≠ z.

Question 9.
(i) The value of the determinant \(\left|\begin{array}{cc}{\sin 10} & {-\cos 10} \\{\sin 80} & {\cos 80}\end{array}\right|\) is
(a) – 1
(b) 1
(c) 0
(d) – 2 (1)
(ii) Using properties of determinants, show that (3)
\(\left|\begin{array}{lll}{a} & {a^{2}} & {b+c} \\{b} & {b^{2}} & {c+a} \\{c} & {c^{2}} & {a+b}\end{array}\right| = (b – c) (c – a) (a – b) (a + b + c)\)
Answer:
(i) (b) Since,
sin 10 cos 80 + cos 10 sin 80 = sin (10 + 80) =sin 90 = 1.

(ii) Let C₃ → C₃ + C₁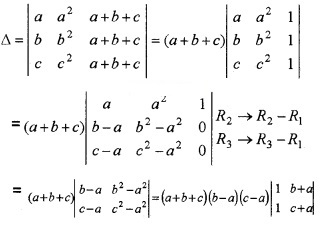

= (a + b + c)(b – a)(c – a)(c + a – b – a)
= (a + b + c)(b – a)(c – a)(c – b)
= (b – c)(c – a)(a – b)(a + b + c).

Question 10.
(i) Choose the correct answer from the bracket. Consider a square matrix of order 3. Let C₁₁, C₁₂, C₁₃ are cofactors of the elements a₁₁, a₁₂, a₁₃ respectively, then a₁₁C₁₁ + a₁₂C₁₂ + a₁₃C₁₃ is (1)
(a) 0
(b) |A|
(c) 1
(d) none of these.
(ii) Verify A(adjA) = (adjA)A = |A|I for the matrix A = \(\left[\begin{array}{ll}{5} & {-2} \\{3} & {-2}\end{array}\right]\) that, where I = \(\left[\begin{array}{ll}{1} & {0} \\{0} & {1}\end{array}\right]\) (3)
Answer:
(i) (b) |A|

(ii) |A| = \(\left|\begin{array}{cc}{5} & {-2} \\{3} & {-2}\end{array}\right|\) = – 4
C₁₁ = – 2, C₁₂ = – 3, C₂₁ = 2, C₂₂ = 5

Hence A(adjA) = (adjA)A = |A|I.

Question 11.
Consider the following system of equations x + 2y = 4,2x + 5y = 9

1. If A = \(\left[\begin{array}{ll}{1} & {2} \\{2} & {5}\end{array}\right]\), find |A| (1)
2. Express the above system of equations in the form AX = B (1)
3. Find adj A, A^-1 (1)
4. Solve the system of equations. (1)

Answer:
1. |A| = \(\left[\begin{array}{ll}{1} & {2} \\{2} & {5}\end{array}\right]\) = 5 – 4 = 1

2. The given system of equation can be expressed in the form AX = B.

3. Cofactor matrix of A = \(\left[\begin{array}{cc}{5} & {-2} \\{-2} & {1}\end{array}\right]\)

4. We have,

x = 2, y = 1.

Question 12.
Consider the point X(-2, -3), B(3, 2), C(-1, -8)

1. Find the area of ∆ABC (2)
2. Find third vertex of any other triangle with same area and base AB. (2)

Answer:
1. \(\frac{1}{2}\left|\begin{array}{ccc}{-2} & {-3} & {1} \\{3} & {2} & {1} \\{-1} & {-8} & {1}\end{array}\right|\)
\(\frac{1}{2}\) (- 2(2 + 8) + 3(3 + 1) + 1(- 24 + 2)) = – 15
Area of ∆ ABC = 15.

2. The base AB is fixed and the third point is variable. Therefore we can choose any x coordinate and find y coordinate or vice versa.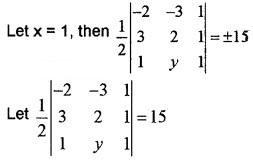

⇒ – 2(2 – y) + 3(3 – 1) + 1(3y – 2) = 30
⇒ – 4 + 2y + 6 + 3y – 2 = 30
⇒ 5y = 30 ⇒ y – 6
Therefore point is(1, 6).

Question 13.
Find the inverse of the following

Answer:
(i) Let |A| = \(\left|\begin{array}{lll}{1} & {2} & {3} \\{0} & {2} & {4} \\{0} & {0} & {5}\end{array}\right|\) = 10
C₁₁ = 10, C₁₂ = 0, C₁₃ = 0, C₂₁ = – 10, C₂₂ = 5, C₂₃ = 0, C₃₁ = – 2, C₃₂ = – 4, C₃₃ = 2

(ii) Let |A| = \(\left|\begin{array}{ccc}{1} & {0} & {0} \\{3} & {3} & {0} \\{5} & {2} & {-1}\end{array}\right|\) = -3
C₁₁ = -3, C₁₂ = 3, C₁₃ = -9, C₂₁ = 0, C₂₂ = -1, C₂₃ = -2, C₃₁ = 0, C₃₂ = 0, C₃₃ = 3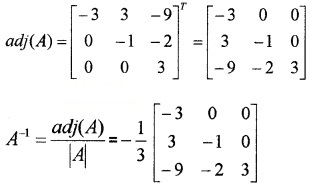

(iii) Let |A| = \(\left|\begin{array}{ccc}{2} & {1} & {3} \\{4} & {-1} & {0} \\{-7} & {2} & {1}\end{array}\right|\)
= 2(-1 – 0) -1(4 – 0) + 3(8 – 7) = -3
C₁₁ = -1, C₁₂ = -4, C₁₃ = 1, C₂₁ = 5, C₂₂ = 23, C₂₃ = -11, C₃₁ = 3, C₃₂ = 12, C₃₃ = -6

(iv) Let |A| = \(\left|\begin{array}{ccc}{1} & {-1} & {2} \\{0} & {2} & {-3} \\{3} & {-2} & {4}\end{array}\right|\)
= 1(8 – 6) + 1(0 + 9) + 2(0 – 6) = -1
C₁₁ = 2, C₁₂ = -9, C₁₃ = -6, C₂₁ = 0, C₂₂ = -2, C₂₃ = -1, C₃₁ = 3, C₃₂ = 3, C₃₃ = 2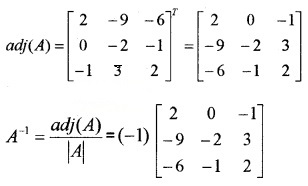

Question 14.
Consider the system of equations 5x + 2y = 4, 7x + 3y = 5. If A = \(\left[\begin{array}{ll}{5} & {2} \\{7} & {3}\end{array}\right]\), X = \(\left[\begin{array}{l}{\mathrm{r}} \\{y}\end{array}\right]\) and B = \(\left[\begin{array}{l}{4} \\{5}\end{array}\right]\)

1. Find |A| (1)
2. Find A^-1 (2)
3. Solve the above system of equations. (1)

Answer:
1. |A| = \(\left|\begin{array}{ll}{5} & {2} \\{7} & {3}\end{array}\right|\) = 15 – 14 = 1.

2. Given, A = \(\left[\begin{array}{ll}{5} & {2} \\{7} & {3}\end{array}\right]\)

3. X = A^-1B

⇒ x = 2, y = -3.

Plus Two Maths Determinants Six Mark Questions and Answers

Question 1.
(i) Let A be a square matrix of order ‘n’ then |KA| = …….. (1)
(ii) Find x if \(\left|\begin{array}{cc}{x} & {2} \\{18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\{18} & {6}\end{array}\right|\) (2)
(iii) Choose the correct answer from the bracket. The value of the determinant \(\left|\begin{array}{ccc}{0} & {p-q} & {p-r} \\{q-p} & {0} & {q-r} \\{r-p} & {r-q} & {0}
\end{array}\right|\) is ….. (1)
(iv) Consider \(\left|\begin{array}{ccc}{a} & {a+b} & {a+b+c} \\{2 a} & {3 a+2 b} & {4 a+3 b+2 c} \\{3 a} & {6 a+3 b} & {10 a+6 b+3 c}\end{array}\right|\) (2)
Answer:
(i) If A be a square matrix of order n, then |KA| = Kⁿ|A|

(ii) \(\left|\begin{array}{cc}{x} & {2} \\{18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\{18} & {6}\end{array}\right|\) ⇒ x² – 36 = 0
⇒ x² = 36 ⇒ x = ±6.

(iii) (c) 0 (since the given determinant is the determinant of a third order skew symmetric matrix)

= a [7a² + 3ab – 6a² – 3ab] = a(a²) = a³

Question 2.
(i) Let \(\left|\begin{array}{lll}{1} & {3} & {2} \\{2} & {0} & {1} \\{3} & {4} & {3}
\end{array}\right|\) = 3, then what is the value of \(\left|\begin{array}{lll}{1} & {3} & {2} \\{4} & {0} & {2} \\{3} & {4} & {3}\end{array}\right|\) = ? and\(\left|\begin{array}{lll}{6} & {7} & {6} \\{2} & {0} & {1} \\{3} & {4} & {3}\end{array}\right| \) = ? (2)
(Hint: Use the properties of determinants)
(ii) Using properties of determinants show that (4)
\(\left|\begin{array}{ccc}{1+a} & {1} & {1} \\{1} & {1+b} & {1} \\{1} & {1} & {1+c}\end{array}\right|=a b c\left(1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Answer: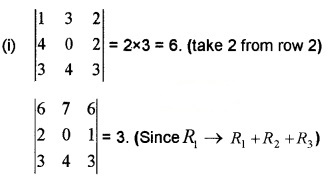

(ii) Taking ‘a’ from R₁, ‘b‘ from R₂,’C’ from R₃

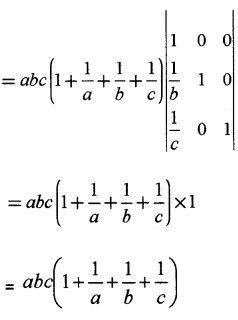
Question 3.
If A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)

1. Find |A| (1)
2. Find adj.A. (2)
3. Solve 2x – 3y + 5z = 11, 3x + 2y – 4z = -5, x + y – 2z = -3 (3)

Answer:
1. A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)
|A| = 2 × 0 + 3x – 2 + 5 = -1.

2. Co.factor A

3. Given

i.e; AX = B ⇒ X = A^-1 B

Question 4.
Let A = \(\left[\begin{array}{ccc}{1} & {-1} & {1} \\{2} & {1} & {-3} \\{1} & {1} & {1}\end{array}\right]\)

1. Is A singular? (1)
2. Find adj A. (2)
3. Obtain A^-1 (1)
4. Using A^-1 solve the system of equations x – y + z = 4, 2x + y – 3z = 0, x + y + z = 2 (2)

Answer:
1. A = \(\left[\begin{array}{ccc}{1} & {-1} & {1} \\{2} & {1} & {-3} \\{1} & {1} & {1}\end{array}\right]\)
⇒ |A| = 4 + 5 + 1 = 10 ≠ 0
A is non singular matrix.

2. Cofactor A

3. A^-1 = \(\frac{1}{10}\) \(\left[\begin{array}{ccc}{4} & {2} & {2} \\{-5} & {0} & {5} \\{1} & {-2} {3}\end{array}\right]\)

4. Given, AX = B ⇒ X = A^-1 B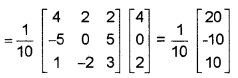

⇒ x = 2, y = -1, z = 1.

Question 5.
Solve the following system of linear equations.

1. x + y + z = 3, y – z = 0, 2x – y = 1 (6)
2. 5x – 6y + 4z = 15 , 7x + 4y – 3z = 19, 2x + y + 6z = 46 (6)
3. x + 2y + 5z = 10, x – y – z = -2, 2x + 3_y-2 = -11 (6)

Answer:
1. Let AX = B
Where A = \(\left[\begin{array}{ccc}{1} & {1} & {1} \\{0} & {1} & {-1} \\{2} & {-1} & {0}\end{array}\right], X=\left[\begin{array}{c}{x} \\{y} \\{z}\end{array}\right], B=\left[\begin{array}{l}{3} \\{0} \\{1}\end{array}\right]\)
|A| = 1(0 – 1) – 1(0 + 2) + 1(0 – 2) = -5
C₁₁ = -1, C₁₂ = -2, C₁₃ = -2, C₂₁ = -1, C₂₂ = 3, C₂₃ = 3, C₃₁ = -2, C₃₂ = 1, C₃₃ = 1

2. Let AX = B,
Where A = \(\left[\begin{array}{ccc}{5} & {-6} & {4} \\{7} & {4} & {-3} \\{2} & {1} & {6}\end{array}\right], X=\left[\begin{array}{c}{x} \\{y} \\{z}\end{array}\right],B=\left[\begin{array}{c}{15} \\{19} \\{46}\end{array}\right]\)
|A| = 5(24 + 3) + 6(42 + 6) + 4(7 – 8) = 419
C₁₁ = 27, C₁₂ = -48, C₁₃ = -1, C₂₁ = -1, C₂₂ = 22, C₂₃ = -17, C₃₁ = 2, C₃₂ = 43, C₃₃ = 62

3. Let AX = B
\(\text { Where } A=\left[\begin{array}{ccc}{1} & {2} & {5} \\{1} & {-1} & {-1} \\{2} & {3} & {-1}
\end{array}\right], X=\left[\begin{array}{c}{x} \\{y} \\{z}\end{array}\right], B=\left[\begin{array}{c}{10} \\{-2} \\{-11}\end{array}\right]\)
|A| = 1(4) – 2(1) + 5(5) = 27
C₁₁ = 4, C₁₂ = -1, C₁₃ = 5, C₂₁ = 17, C₂₂ = -11, C₂₃ = 1, C₃₁ = 3, C₃₂ = 6, C₃₃ = -3

⇒ x = -1, y = -2, z = 3.

Question 6.
If f(x) = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\{\sin x} & {\cos x} & {0} \\{0} & {0} & {1}\end{array}\right]\)
(i) Find f(-x) (2)
(ii) Find (f(x)]^-1 (2)
(iii) Is |f(x)]^-1 = f(-x)? (2)
Answer:

(ii) |f(x)| = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\{\sin x} & {\cos x} & {0} \\{0} & {0} & {1}\end{array}\right]\) = cos x (cos x) + sin x (sin x) = 1 ≠ 0
Therefore , [f(x)]^-1 exists.
The cofactors are as follows.
C₁₁ = cos x, C₁₂ = -sin x, C₁₃ = 0, C₂₁ = sin x, C₂₂ = cos x, C₂₃ = 0, C₃₁ = 0, C₃₂ = 0, C₃₃ = 1

Since, |f(x)|= 1

(iii) Yes. From (1) and (2) we have,
[f(x)]^-1 =f(-x).

Question 7.
(i) Choose the correct answer from the bracket. If A = \(\left[\begin{array}{cc}{2} & {3} \\{1} & {-2}\end{array}\right]\) and A^-1 = kA, then the value of ‘k’ is
(a) 7
(b) -7
(c) \(\frac{1}{7}\)
(d)\(-\frac{1}{7}\) (1)
(ii) If A = \(\left[\begin{array}{ccc}{1} & {-1} & {1} \\{2} & {-1} & {0} \\{1} & {0} & {0}
\end{array}\right]\),
(a) A² (2)
(b) Show that A² = A^-1 (3)
Answer:

C₁₁ = 0, C₁₂ = 0, C₁₃ = 1, C₂₁ = 0, C₂₂ = -1, C₂₃ = -1, C₃₁ = 1, C₃₂ = 2, C₃₃ = 1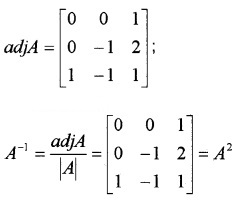

Question 8.
‘Arjun’ purchased 3 pens, 2 purses, and 1 instrument box and pays Rs. 410. From the same Shop ‘Deeraj’ purchases 2 pens, 1 purse, and 2 instrument boxes and pays Rs.290, while ‘Sindhu’ purchases 2pens, 2 purses, 2 instrument boxes and pays Rs. 440.

1. Translate the equation into system of linear equations. (2)
2. The cost of one pen, one purse and one instrument box using matrix method. (4)

Answer:
1. Let The price of one pen is Rs.x, one purse is Rs.y and one instrument box be Rs.z
3x + 2y + z = 410; 2x + y + 2z =290; 2x + 2y + 2z = 440(1) 2 mts.

2. The system can be represented by the matrix equation AX = B

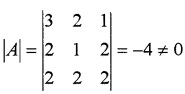
C₁₁ = -2, C₁₂ = 0, C₁₃ = 2, C₂₁ = -2, C₂₂ = 4, C₂₃ = -2, C₃₁ = 3, C₃₂ = -4, C₃₃ = -1

Hence the cost one pen is Rs.20, one purse is Rs. 150 and one instrument box is Rs. 50.

Question 9.
If A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)

1. Find A^-1 (3)
2. Using it solve the system of equations 2x – 3y + 5z = 16, 3x + 2y – 4z = -4, x + y – 2z = -3 (3)

Answer:
1. A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\{3} & {2} & {-4} \\{1} & {1} & {-2}\end{array}\right]\)
⇒ |A| = 0 + 3x – 2 + 5 = -1

2. Given AX = B
⇒ X = A^-1B

⇒ x = 2, y = 1, z = 3.

Question 10.
Consider the following system of equations x + y + 3z = 5, x + 3y – 3z = 1, -2x – 4y – 4z = -10
(i) Convert the given system in the form AX = B (1)
(ii) Find A^-1 (3)
(iii) Hence solve the system of equations. (2)
Answer:

(ii) i.e; AX = B, ⇒ X = A^-1 B ⇒ |A| = -24 + 10 + 6 = -8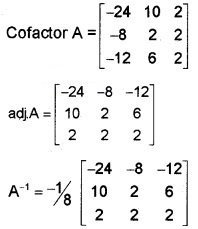

(iii) X = A^-1B

= \(-\frac{1}{8}\) \(\left[\begin{array}{l}{-8} \\{-8} \\{-8}\end{array}\right]\)
⇒ x = 1, y = 1, z = 1.

Question 11.
Solve the following system by equations by matrix method x + 2y + 5z = 10; x – y – z = -2; 2x + 3y – z = -11.
Answer:
x + 2y + 5z = 10; x – y – z = -2; 2x + 3y – z = 11

⇒ x = -1, y = -2, z = 3.

Question 12.
If A = \(\left[\begin{array}{ccc}{3} & {-2} & {3} \\{2} & {1} & {-1} \\{4} & {-3} & {2}\end{array}\right]\)

1. Find |A| (1)
2. Find A^-1 (3)
3. Solve the linear equations 3x – 2y + 3z = 8; 2x + y – z = 1; 4x – 3y + 2z = 4 (2)

Answer:
1. |A| = \(\left[\begin{array}{ccc}{3} & {-2} & {3} \\{2} & {1} & {-1} \\{4} & {-3} & {2}\end{array}\right]\)
= 3(2 – 3) + 2(4 + 4) + 3(- 6 – 4) = -17.

2. |A| ≠ 0, hence its inverse exists.
A^-1 = \(\frac{1}{|A|}\)adj A
C₁₁ = -1, C₁₂ = -8, C₁₃ = -10, C₂₁ = -5, C₂₂ = -6, C₂₃ = 1, C₃₁ = -1, C₃₂ = 9, C₃₃ = 7

3. The given system of linear equations is of the form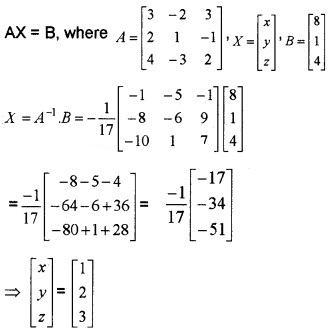

∴ We have, x = 1, y = 2, z = 3.

Question 13.
if \(\left[\begin{array}{cc}{2} & {5} \\{-3} & {7}\end{array}\right] \times A=\left[\begin{array}{cc}{17} & {-1} \\{47} & {-13}\end{array}\right]\) then
(i) Find the 2 × 2 matrix A. (3)
(ii) Find A². (1)
(iii) Show that A² + 5A – 6I = 0, where I is the identity matrix of order 2. (2)
Answer: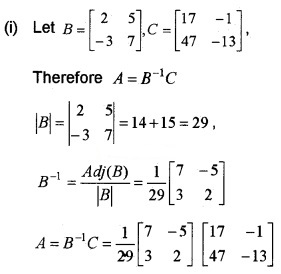

Plus Two Mathematics All Chapters Question and Answers

• Plus Two Mathematics Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 1 Relations and Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 2 Inverse Trigonometric Functions Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 3 Matrices Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 5 Continuity and Differentiability Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 6 Application of Derivatives Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 7 Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 8 Application of Integrals Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 9 Differential Equations Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 10 Vector Algebra Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 11 Three Dimensional Geometry Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 12 Linear Programming Chapter Wise Question and Answers PDF
• Plus Two Maths Chapter 13 Probability Chapter Wise Question and Answers PDF

Benefits of the Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF

The Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF that has been provided above is extremely helpful for all students because of the way it has been drafted. It is designed by teachers who have over 10 years of experience in the field of education. These teachers use the help of all the past years’ question papers to create the perfect Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF.

FAQ’s Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF

Where can I download Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF?

You can download Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF for the latest 2021 session.

Can I download Plus Two All subjects Question and Answers PDF?

Yes - You can click on the links above and download subject wise question papers in PDF

Is there any charge for the Plus Two Maths Chapter 4 Determinants Chapter Wise Question and Answers PDF?

There is no charge for the model papers for you can download everything free